Assessing Computational Thinking

by
Back to Primers

Authors: Quinn Burke, Cinamon Sunrise Bailey, and Pati Ruiz
Printer-Friendly PDF | Google Doc for Comments | Questions? Contact CIRCL.

Overview


From Angevine, C. (2017). Advancing computational thinking across K-12 education. [Blog post].

Computational thinking (CT) is increasingly being recognized as a crucial educational literacy characteristic of 21st century learning as well as a requisite skill for the 21st century economy, which relies on computing as an essential component of commerce. CT is broadly defined as a way of “solving problems, designing systems and understanding human behavior by drawing on the concepts fundamental to computer science” (Wing, 2006, p. 33).The term “computational thinking” can be dated back to the 1980s when Seymour Papert’s Mindstorms book brought to the mainstream the idea of using computers in K-12 schools as “objects to think with”. However, it was Jeannette Wing’s influential 2006 article on CT that helped spark CT as an educational imperative for schools. Since 2006, a total of forty (40) states have enacted–or are in the process of enacting–computer science (CS) standards and frameworks for their K-12 schools (Code.org, 2018). In high school, CS is typically a stand-alone course offering; however, on the K-8 levels, many states and districts are largely focusing on integrating computing into existing coursework, be it math, science, social studies, and/or language arts. With this curricular integration on K-8 levels, the goal is twofold: First, to foster children’s capacity to formulate and address problems systematically; and second, to direct and reinforce learning within existing academic disciplines through the refinement of such problem solving skills.

One of the primary challenges of computational thinking as an integrative, cross disciplinary competency is of assessment. In assessing CT, one could consider evaluating a student with regards to any or all of the three dimensions of CT:

  1. computational concepts: the fundamental concepts students engage with as they program or engage in CT oriented practices-such as algorithmic thinking, decomposition, abstraction, parallelism, and pattern generalization
  2. computational practices: the actual practices students develop as they encounter and engage with the concepts; this includes collecting and sorting data, designing and remixing computational models, debugging simulations, documenting one’s work, and collaboratively breaking down complex problems to their requisite parts
  3. computational perspectives: the perspectives students form about the world around them and about themselves as they comprehend these concepts and engage in such practices; perspectives here refers to learners’ own sense of agency and technology fluency, as well as a wider appreciation as to how systems function, why they break down and how they can be improved

Given the imperative to integrate CT into existing school subjects, especially on the K-8 levels, there are questions as to how to define CT as a skill and as a knowledge. Is CT best assessed as a series of learned concepts? How does understanding such concepts measurably inform CT practices? How does CT learning transfer across academic subject areas and how does its subject matter integration inform the dimensions of CT that can be be assessed? Alongside these pressing questions, there are then other persistent variables to consider that are characteristic of assessing any type of learning. How do teaching practices and purported learning styles inform the way CT is assessed, and how do these assessments relate to grade level expectations and expected competencies?

There is general consensus from the research (Aiken et al., 2012; Dorling, 2016; Duncan, 2018; Grover, Cooper, & Pea, 2014; Grover & Pea, 2013; Snow et al., 2012; & Wentrop et al., 2015) that computational thinking represents a more robust and practical goal for K-12 schools than the more nebulous goal of “digital literacies”, which too often is driven by for-profit companies promoting particular apps and products.

Yet there is still considerable debate over the precise meaning of computational thinking, and much of this stems directly back to this question of effective and consistent assessment. Being able to effectively assess CT within different content areas allows for a greater understanding as to how it may best be implemented into a range of academic content areas. More rigorous and systematic assessment also could inform what pedagogies better facilitate learners’ understanding of its various components. In the same manner, changes could be made to the wider school curricula in order to address changing student and workforce needs. Finally, gaining a stronger grasp on the ways and means CT is (and could be) assessed offers a sharper examination of equity of access and educational experience within schools with regards to which students are encountering such content and to the degree they are comprehending it.

Key Lessons

The following lessons stem from research that has been conducted regarding defining and assessing CT concepts, CT practices, and CT perspectives:

Assessing Computational Concepts

Researchers have defined several CT concepts that are highly useful when students/designers understand them and are able to apply them in various academic and non-academic contexts:

iterative, recursive, and parallel thinking; sequences; loops; events; conditionals; operators; data; abstraction; evaluation; algorithmic thinking/design; decomposition; automation; pattern generalization; pattern recognition; systematic processing of information; symbol systems and representations; conditional logic; efficiency and performance constraints; debugging; and systematic error detection (Basu, Mustafaraj, & Rich, 2016; Brennan & Resnick, 2012; Grover & Pea, 2013)

Methods for Measuring CT Concepts. Guided by their design of the Three-Dimensional Integrated Assessment (TDIA) framework, Zhong, Wang, and Chen (2016) developed assessment tasks that aimed to comprehensively assess the three dimensions of CT: computational concepts, practices, and perspectives. There have been several methods proposed for measuring CT concepts. These include:

Designed based assessments and/or software engineering metrics:

  • Dr. Scratch, a free, open source software assessment tool for Scratch; Fairy Performance Assessment as an Alice program to analyze thinking algorithmically and making effective use of abstraction and modeling (Werner, Denner, Campe, & Kawamoto, 2012); REACT-Real Time Evaluation and Assessment of Computational Thinking (Koh, Basawapatna, Nickerson, & Repenning, 2010); Bebras tasks-aimed at choosing interesting tasks, which motivate learners to deal with informatics and to think deeper about technology (Román-González, Moreno-León, & Robles, 2017)

Accumulative content knowledge based assessments:

  • Computational Thinking Test (CTt): designed for primary and middle school; aligned with the CSTA Computer Science Standards for the 7th and 8th grade; multiple choice; each item measures one or more of seven computational concepts; this has been used in content area research (i.e. language arts) (Román-González, 2015; Román-González, Pérez-González, & Jiménez-Fernández, 2016; Román-González, Pérez-González, & Jiménez-Fernández, 2017)
  • Commutative Assessment Test: evaluate “if and how programming modality affects learnability”. (Weintrop & Wilensky, 2015, p.4)

Assessment of computational language/vocabulary as a measurement of CT conceptual knowledge

Surveys/Interviews/Feedback forms:

  • Artifact-Based interviews (Brennan and Rosnick, 2012); questionnaires, journal entries, and semi-structured interviews (Chalmers, 2018); Relational Screening Model: “Personal Information Form” (Durak & Saritepeci, 2017); The CTP Video-Prompt Survey (Marsall, 2011); and teacher feedback through online forms (Duncan, 2018)

Assessing Computational Practices

CT skills can be applicable across disciplines. For example, a student studying Spanish could identify patterns in word and sentence structure, compare these patterns to ones that could be found in English, and then explain the similarities and differences in these patterns to a classmate. These are skills that can be classified as ‘systems thinking’ CT practices.

By transferring CT skills and practices across school subjects, students ought to be able to use different approaches and perspectives in order create more innovative solutions in other fields, including language arts, science, mathematics, social science, and humanities. Researchers have organized CT Practices into the following areas:

Data practices (collecting data, creating data, manipulating data, logically organizing and analyzing data, visualizing data)

Modeling and simulation practices (using computational models to understand a concept, using computational models to find and test solutions, assessing computational models, designing and drafting computational models)

Computational problem solving practices (formulating problems in a way that enables us to use a computer and other tools to help solve them, choosing effective computational tools, approaching the problem using programmatic thinking techniques, assessing different approaches/solutions to a problem, breaking down problems into manageable components, generalizing this problem-solving process to a wide variety of problems, developing modular computational solutions, creating computational abstractions, troubleshooting and debugging)

Systems thinking practices (investigating a complex system as a whole, understanding the relationship within a system, thinking in levels, communicating information about a system, generalizing and transferring this problem solving process to a wide variety of problems, defining systems and managing complexity)

Methods for Measuring CT Practices. There have been several methods proposed for measuring CT practices. These include:

CT skill-transfer: aimed at assessing the students’ transfer of their CT skills to different types of problems

  • Bebras Task measures transfer to ‘real life’ problems (Dagiene & Futschek, 2008)
  • CTP-Quiz: analyzes the transfer of CT to the context of scientific simulations (Basawapatna, Koh, Repenning, Webb, & Marshall, 2011)

Student-generated portfolios & rubrics

  • Project portfolio analysis (Brennan & Rosnick, 2012)
  • Rubrics designed to evaluate student work across five dimensions: general factors, design mechanics, user experience, basic coding constructs, and advanced coding constructs (Grover, Basu, & Schank, 2018)

Audio and video capture/observation of Students engaged in CT practices

Direct observation of student performances using field notes to document progress

Assessments based on real-time manual input (i.e. keystroke/ time spent on task)

Assessing Computational Perspectives

As students interact and participate with CT tools and artifacts, their relationships to others as well as the world around them purportedly evolves. CT attitudes and perspectives involve elements related to that evolving understanding of self that students experience. Basically, it is how a student sees themselves, their relationship with others, and the computational thinking world around them.

Engaging students in computational thinking practices could help develop their perspectives/ dispositions, which can then potentially enhance their academic and career success. The Computer Science Teachers Association (CSTA) and the International Society for Technology in Education (ISTE) (2011) identify “confidence in dealing with complexity, persistence in working with difficult problems, tolerance for ambiguity, the ability to deal with open-ended problems, and the ability to communicate and work with others to achieve a common goal or solution” as dispositions or attitudes that are essential dimensions of CT.

Method for Measuring CT Perceptions. Examples of methods proposed for measuring CT perceptions include:

CT Perceptions-Attitudes scales/tests/rubrics

  • Computational Thinking Scales (CTS): five-point Likert scale; examines creativity, algorithmic thinking, cooperativity; critical thinking; and problem solving (Korkmaz, Çakir, & Özden, 2017). Though this study was done in a turkish post-secondary setting, it did show validity.
  • The Computational Thinking Test (CTt) as a means to predict if ‘computationally talented’ students can be detected prior to learning a CT task (can levels of success be predicted prior to learning and how can this contribute to the development of more individualized lesson plans) (Román-González, Pérez-González, Moreno-León, & Robles, 2018)
  • Rubric on learning dispositions (Dorling, 2016)
  • Self-efficacy survey five point Likert scale: assesses problem solving skills and ability to think computationally (Weese & Feldhausen, 2017)

Computational Thinking Pattern Analysis (CTPA): implements computational thinking patterns in a student-created game and uses the game’s tutorial “norm” as a gauge of creativity. (Bennett, Koh, & Repenning, 2013)

Issues

While computational thinking is increasingly being recognized as a crucial skill for K-12 students, there are a number of challenges associated with its integration into schools and effectively assessing it.

CT Definitions. First, as noted earlier, there is still a lack of consensus with regards to how to define CT knowledge and skill acquisition. Do students have to demonstrate knowledge and abilities in all dimensions of CT (concepts, practices, and perspectives), or are we able to ascertain that they have CT knowledge/skills if they only obtain/express partial knowledge in one domain? For example, if a student is able to analyze data but has not displayed knowledge of systems-thinking practices (investigating a complex system as a whole, understanding the relationship within a system, and managing complexity), can we still say this student has CT knowledge even though they have only displayed knowledge/skills in data practice? More research needs to occur in order to develop a shared understanding and vocabulary of what computational thinking encompasses.

Multiple CT Dimensions. Second, while an exact definition of CT is still a matter of debate, as the prior section details, there has been wider consensus that CT entails concepts, practices, and perspectives. Accordingly, to assess a student or program with regards to only one of these dimensions provides an incomplete picture of CT. In developing and articulating a computational thinking framework, all three of the dimensions of CT ought to be addressed. In this regard, multiple means of assessments (i.e., artifact analysis, surveys, field note observations) may very well be necessary in order to fully evaluate a student’s nascent CT knowledge and abilities. Without this, there is a risk of missing key pieces of information and contributing factors, which could affect CT development and implementation (i.e. cognitive and personality traits, learning styles, age and gender specific factors, environmental effects, and curriculum contributions).

Correlations between CT Dimensions. Third, studies evaluating the acquisition of CT increasingly need to consider correlation between conceptual knowledge, practical application, and wider shifts in personal perspectives. If a student successfully completes an activity, does this simultaneously demonstrate understanding of the CT concept as well as the achievement of a particular CT practice and a broader understanding of computing’s role in society? At this point, with assessing CT still in a fledgling stage, researchers have a responsibility for developing metrics for each of these dimensions and examining to what degree conceptual gains correspond to documented changes in practice and personal perspectives. Arguably the second dimension related to CT practices is the most difficult to document and ascertain. Conceptual understanding can be often be gauged by the analysis of student projects as well as through simple quizzes and puzzles related to particular CT concepts. Pre-and post surveys coupled with participant interviews meanwhile capture shifts in perspectives. Assessing actual practice however relies heavily on direct observation and field note documentation, which is especially labor-intensive and time-consuming. Real-time digital assessments, such as documenting participants’ keystrokes and the time spent online on a particular task, offer more immediate sources of data around practices, but these require considerable analyses on the back-end and are rarely telling metrics without corresponding measures, such as artifact analysis and participant survey responses.

Integrating CT into Curriculum. Finally, while the question of skills transfer is not a new one, it has renewed significance as schools are increasingly attempting to integrate CT across a range of academic subject areas. While there are numerous studies documenting CT’s integration into math, science, ELA, and social sciences coursework, we still altogether lack substantial research how to optimally integrate CT into the curriculum and how to assess it in terms of the content area with which it is aligned. Additional questions could include asking to what degree CT can or should be assessed as a distinct skill set, as a series of goal-directed activities or regulatory processes, and/or as part of the normal formative and summative assessment processes that are already occurring within an academic content area.

Projects & People

Examples of NSF Cyberlearning projects that overlap with topics discussed in this primer.

Computational Thinking

Other related projects:

Related CIRCL Perspectives:

  • Marie Bienkowski – NSF Project: Principled Assessment of Computational Thinking; Investigators: Eric Snow, Marie Bienkowski
  • Deborah Fields – NSF Project: EXP: Macro Data for Micro Learning: Developing FUN! for Automated Assessment of Computational Thinking in Scratch; Investigators: Deborah Fields, Sarah Brasiel, Taylor Martin
  • Mark Guzdial – Course and tool development for CS1 Course: Media Computation; FCS1 (with student, Allison Elliott Tew), the first validated test of introductory CS knowledge designed to be multilingual; replicated by SCS1 (with student, Miranda Parker)
  • Yasmin Kafai – NSF Project: Collaborative Research: ET-ECS: Electronic Textiles for Exploring Computer Science with High School Students and Teachers to Promote Computational Thinking and Participation for All; Investigators: Yasmin Kafai, Jane Margolis, Joanna Goode
  • Pati Ruiz – also see her CIRCLEducator blog posts including a review of the 2016 NSF Video Showcase: Broadening Participation
  • Aman Yadav – NSF Project: PD4CS (Professional Development for Computer Science); CPATH-2: Computer Science Pathways for Educators

Resources

Related CIRCL Primers:

Conferences & Organizations:

  • AERA SIG/ATL and SIG/LS – Special Interest Groups in Advanced Technologies for
    Learning and Learning Sciences
  • CSforAll – Resources for districts, schools, and classrooms to help provide all K-12 students with an effective computer science education.
  • CSTA – Computer Science Teachers Association
  • Code.org – Online resource for learning and teaching coding practices (aim: increase access to computer science in schools)
  • ICLS – International Conference of the Learning Sciences
  • ISTE – The International Society for Technology in Education
  • K12CS – K–12 Computer Science Framework
  • RESPECT – Research on Equity and Sustained Participation in Engineering, Computing, and Technology
  • SIGCSE – Special Interest Group on Computer Science Education

Videos:

Digital Media:

Tools:

Computational Thinking Frameworks:



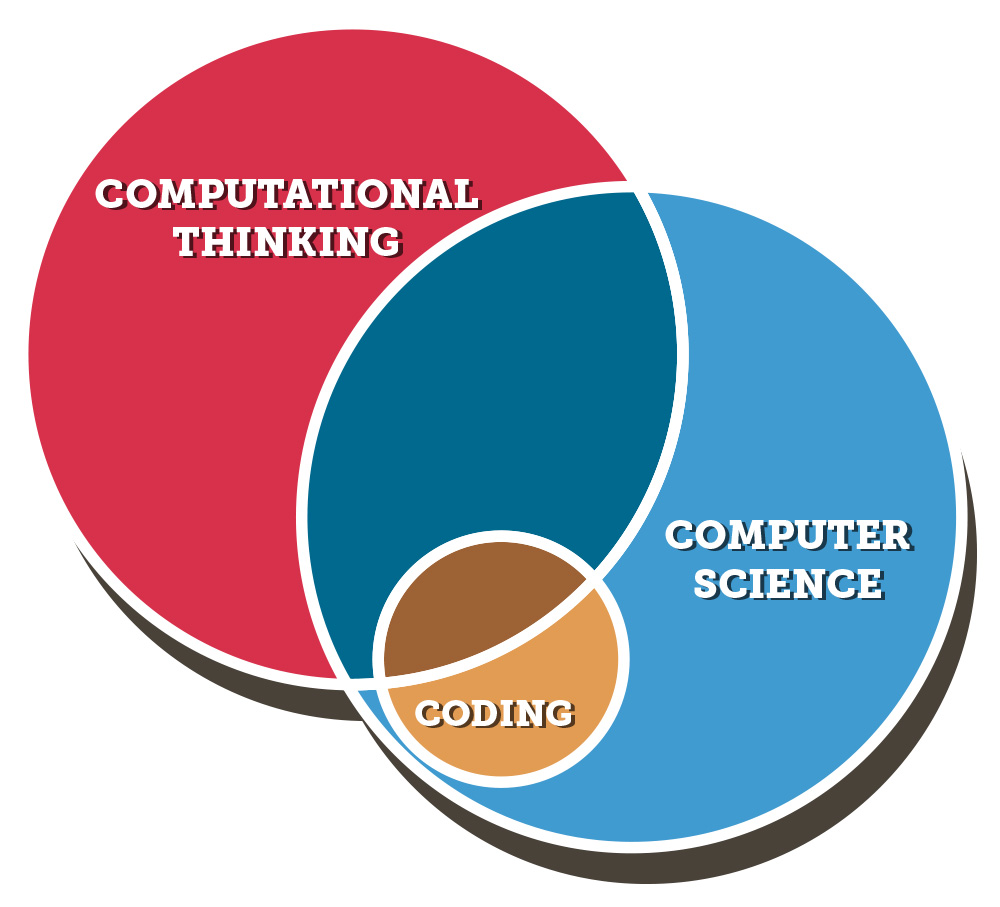
From presentation by P. McLaren & J. Sole


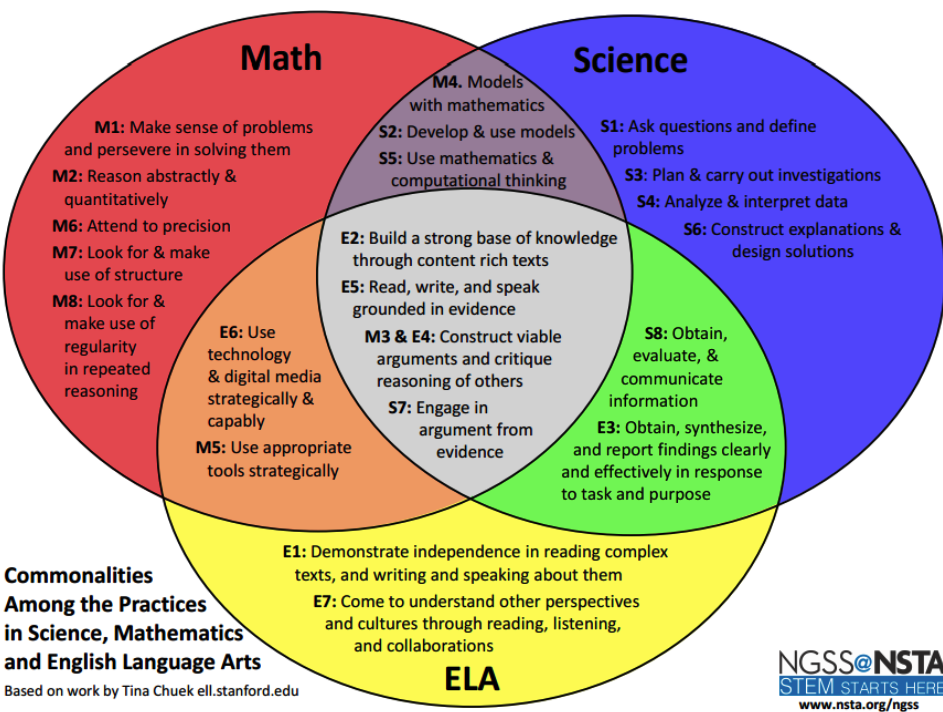
From Angevine, C. (2017). Advancing computational thinking across K-12 education. [Blog post].


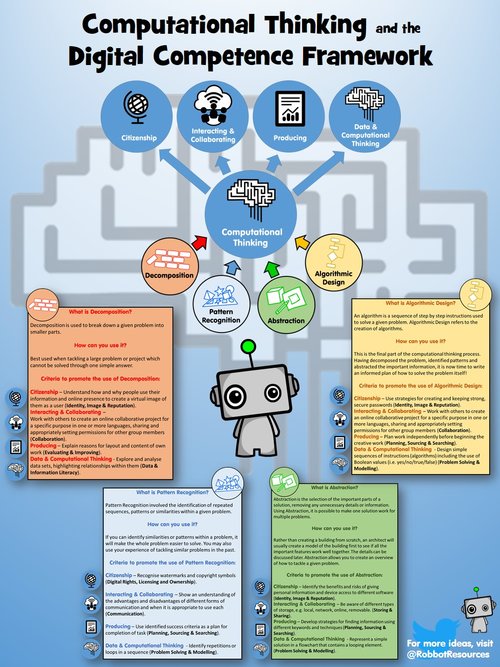
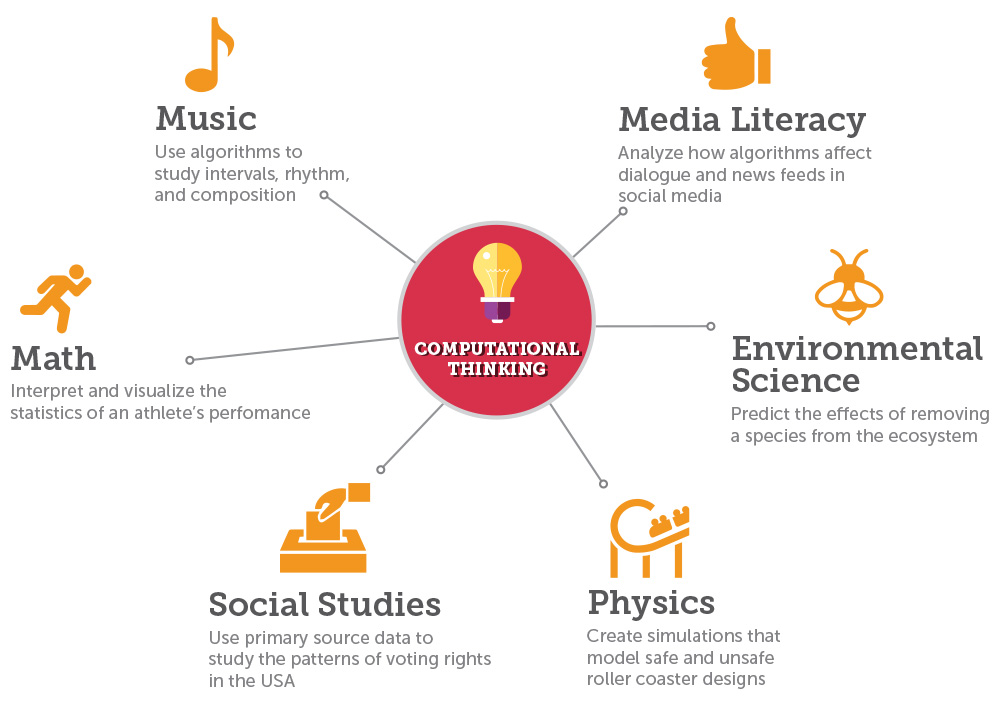
From Rob-Bot Resources

Readings

References and key readings used in this primer on the dimensions of CT thinking (concepts,
perspectives, and practices) as well as research on assessment in these areas are listed below.

Aiken, J.M., et al. (2012). Understanding student computational thinking with computational modeling. In Proceedings PERC ’12 Physics Education Research Conference. Philadelphia, PA, USA.

Assaf, D. et al. (2016). Retention of flow: Evaluating a computer science education week activity. In SIGCSE ’16, The 47th ACM Technical Symposium on Computing Science Education. Memphis, TN, USA

Basawapatna, A., Koh, K. H., Repenning, A., Webb, D. C., & Marshall, K. S. (2011). Recognizing computational thinking patterns. In Proceedings of the 42nd ACM technical symposium on Computer science education (pp. 245–250).

Basu, S., Mustafaraj, E., & Rich, K. (2016). CIRCL primer: Computational thinking. In CIRCL Primer Series. Retrieved from http://circlcenter.org/computational-thinking

Basu, S., Biswas, J., & Kinnebrew, J.S. (2017). Learner modeling for adaptive scaffolding in a
computational thinking-based science learning environment. User Modeling and User-Adapted Interaction Archive, 27 (1), 5-53.

Bennett, V.E., Koh, K. & Repenning, A. (2013). Computing creativity: Divergence in computational thinking. In Proceedings of the 44th ACM tech

Brennan, K. & Resnick, M. (2012). Using artifact-based interviews to study the development of computational thinking in interactive media design. Paper presented at AERA ’12: Annual American Educational Research Association Meeting. Vancouver, BC, Canada.

Chalmers, C. (2018). Robotics and computational thinking in primary school. International Journal of Child-Computer Interaction, 17, 93-100.

Code.org (2018). Landscape of CS Action in states.

Dagiene, V., & Futschek, G. (2008). Bebras international contest on informatics and computer literacy: Criteria for good tasks. In International Conference on Informatics in Secondary Schools-Evolution and Perspectives (pp. 19–30).

Dorling, M. (2016). Computational Thinking rubric: learning behaviours, dispositions and perspectives. A rubric for computational thinking learning behaviours (practices), dispositions and perspectives.

Duncan, C. (2018). Reported development of computational thinking, through computer science and programming, and its benefits for primary school students. In SIGCSE ’18: Proceedings of the 49th ACM Technical Symposium on Computer Science Education, Baltimore, Maryland, U.S.A.

Durak, H.Y., & Saritepeci, M. (2017). Analysis of the relation between computational thinking skills and various variables with the structural equation model. Computers & Education, 116, 191-202.

Grover, S. & Pea, R. (2013). Using a discourse-intensive pedagogy and android’s app inventor for introducing computational concepts to middle school students. Proceedings from SIGCSE ’13: The Changing Face of Computing. Denver, CO: USA.

Grover, S., Cooper, S., & Pea, R. (2014). Assessing computational learning in K-12. Proceedings from ITiCSE ’14: Conference on Innovation & Technology in Computer Science Education. Uppsala, Sweden.

Grover, S. & Pea, R. (2013). Computational thinking in k−12: A review of the state of the field. Educational Researcher, 42 (38).

Grover, S., Basu, S., & Schank, P. (2018). What we can learn about student learning from open-ended programming projects in middle school computer science. In SIGCSE ’18: 49th ACM Technical Symposium on Computer Science Education. Baltimore, MD: USA.

Koh, K.H., Basawapatna, A.,Nickerson, H., & Repenning, A. (2010). Real time assessment of computational thinking. In Proceedings from IEEE ’14. Symposium on Visual Languages and Human-Centric Computing (VL/HCC). Melbourne, Australia.

Kong, S.C., Chiu, M.M., & Lai, M. (2018). A study of primary school students’ interest, collaboration attitude, and programming empowerment in computational thinking education. Computers & Education, 127, 178-89.

Korkmaz, O., Çakir, R., Ozden, M.Y. (2017). A validity and reliability study of the computational thinking scales (CTS). Computers in Human Behavior, 72, 558-569.

Marsall, K.S. (2011). Was that CT? Assessing computational thinking through video-based prompts. In AERA ’11: Annual Meeting of the American Educational Association. New Orleans, Louisiana, USA.modeling. In Proceedings PERC ’12 Physics Education Research Conference. Philadelphia, PA, USA.

Román-González, M. (2015). Computational Thinking Test: Design Guidelines and Content Validation. In Proceedings of the 7th Annual International Conference on Education and New Learning Technologies (EDULEARN 2015) (pp. 2436–2444).

Román-González, M., Pérez-González, J.C., & Jiménez-Fernández, C. (2016). Which cognitive abilities underlie computational thinking? Criterion validity of the Computational Thinking Test. Computers in Human Behavior.

Román-González, M., Pérez-González, J. C., & Jiménez-Fernández, C. (2017). Which cognitive abilities underlie computational thinking? Criterion validity of the Computational Thinking Test. Computers in Human Behavior, 72, 678–691.

Román-González, M., Moreno-León, J., & Robles, G. (2017). Complementary tools for computational thinking assessment. In Proceedings International Conference on Computational Thinking Education 2017, Hong Kong, China.

Román-González, M., Pérez-González, J. C., Moreno-León, J., & Robles, G. (2018). Can computational talent be detected? Predictive validity of the Computational Thinking Test. International Journal of Child-Computer Interaction.

Snow, E., et al. (2012). Assessing computational thinking. In NSF-CE21 Community Meeting. Washington, DC, USA

Weese, J.L. & Feldhausen, R. (2017). STEM outreach: Assessing computational thinking and problem solving. ASEE ’17: Annual Conference and Exposition American Society for Engineering Education, Curricular issues in computing,

Weintrop, D., & Wilensky, U. (2015). Using Commutative Assessments to Compare Conceptual Understanding in Blocks-based and Text-based Programs. In ICER (Vol. 15, pp. 101–110).

Weintrop, D. et al. (2015). Defining computational thinking for mathematics and science
classrooms. Journal of Science and Educational Technology.

Werner, L., Denner, J., Campe, S., & Kawamoto, D.C. (2012). The fairy performance assessment: measuring computational thinking in middle school. Proceedings from SIGCSE’12: 43rd ACM Technical Symposium on Computer Science Education. Raleigh, North Carolina, USA.

Wing, J. M. (2006). A vision for the 21st century: Computational thinking, Communications of the ACM, 49(3), 33-35.

Yarnall, L. & Haertel, G. (2016). CIRCL primer: Evidence-Centered Design. In CIRCL Primer Series.

Zhong, B., Wang, Q., Chen, J., & Li, Y. (2016). An exploration of three-dimensional integrated assessment for computational thinking. Journal of Educational Computing Research, 53(4), 562–590.

Citation

Primers are developed by small teams of volunteers and licensed under a Creative Commons Attribution 4.0 International License. After citing this primer in your text, consider adding: “Used under a Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/).”

Suggested citation:

Burke, Q., Bailey, C. S., & Ruiz, P. (2019). CIRCL Primer: Assessing Computational Thinking. In CIRCL Primer Series. Retrieved from http://circlcenter.org/assessing-computational-thinking

Special thanks to Kerri-Anne O’Donnell and Patricia Schank for reviewing and suggesting edits to this primer.